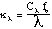
Predictions are compared to measured values and to previous empirical models of coal-derived soot. Reasonable correlation exists between measurements and the predictions of the new model.
Introduction
Computational Fluid Dynamics (CFD) codes, with the advent of powerful computers, have recently become increasingly popular design tools. Comprehensive models have the capability of predicting many important details of complex combustion problems.
An ongoing project at BYU is the modeling of coal reactors, and considerable effort has been spent to develop a comprehensive computer model for coal combustion called Pulverized Coal Gasification and Combustion in 3 dimensions (PCGC-3). This model is capable of predicting temperature, pressure, particle path, energy transport, and chemistry in a turbulent coal-fired reactor. It also uses the Chemical Percolation Model for Devolatilization (CPD model) to determine tar and total volatile yields (Fletcher et al., 1992). The ability to accurately predict such parameters can aid in reactor design by allowing computer testing and optimization of new designs or modifications.
One important part of the code is the prediction of radiative transport due to particles and gases within the flames. The radiative transport equation (RTE) is generally used to solve for the radiative heat transfer in a semi-transparent media. In order to make proper calculations, information regarding the radiative properties of the medium need to be calculated. Soot, or the polycyclic aromatic hydrocarbon particulates formed during coal combustion, can be a major contributor to the radiative transport. Some calculations indicate that soot can contribute as much as fifteen percent to the total radiative flux (Ahluwalia and Im, 1994).
Other research indicates that temperature predictions in certain combustor locations can vary by as much as several hundred degrees K based on the inclusion of soot predictions (Kollmann et al., 1994 and Adams and Smith, 1995). While this may not be important for the overall energy balance in a combustor, it may be more important for pollutant calculations. Minor changes in temperatures can make a significant impact on pollutant formation predictions, which tend to be highly temperature dependent. Since the near burner region is of great interest to pollutant prediction calculations, and it also tends to be the region of maximum soot, predicting the radiative contribution of soot becomes even more important.
Background
Since the effect of soot radiation is significant, attempts have been made to account for the phenomena. Unagglomerated soot is generally considered to be non-scattering. This indicates that the primary mode of thermal radiation attenuation is absorption. The spectral absorption coefficient is used to describe absorption in a gaseous medium within the RTE. For most gases, this value may be measured by simply passing a length of monochromatic light through the gas with a known density. This cannot be done accurately for soot because the soot in the flame is not a gas, and generally undergoes rapid chemical changes. A frequently referenced, simplified method for estimating the absorption coefficient of soot is discussed in detail by Siegel and Howell (1992):
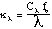
In this equation, C sub lambda is a constant developed from Mie theory for spheres which is dependent on the complex index of refraction, fv is the volume fraction of soot, and lambda is the wavelength of the radiation. Sarofim and Hottel (1978) developed a more simple model for the determination of the emissivity of soot disregarding the spectral effects. Their gray gas assumption is:
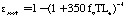
The emissivity may be related to the absorption coefficient kappa through Bouguer's Law:
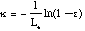
to give:
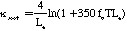
Where kappa sub soot is the emissivity of soot, T is temperature in Kelvin, and Le is the mean beam length in the furnace. Following Kent and Honnery (1990) by combining Equations 1 and 3, weighting by the Plank function, and numerically integrating:
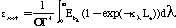
The two soot radiative properties models are compared in Figure 1.
Several researchers have indicated that approximate values of C sub lambda for most soot ranges from 3-7. A recent comparison of optical properties of soot measurements taken from several different researchers shows significant variability (Menguc and Webb, 1993). Recent measurements by Majidi et al. (1994) using gas derived soot and Rigby (1996) using coal soot have indicated that the optical properties for soot may vary significantly depending on the chemistry of the fuel of origin. This implies that an accurate estimation of the soot radiative properties may require detailed information regarding the chemistry of the soot, which is currently unavailable and beyond the scope of most practical modeling efforts.
Determining the volume fraction of soot is also very difficult. Soot is thought to exist in the largest quantities in the fuel-rich region of flames. Efficient flames will burn off the soot, leaving little or no soot outside of the flame region. Several variables are thought to affect the soot volume fraction. In gas flames, acetylene is understood to be a precursor to soot. Unlike gas flames, soot in coal flames is thought to mostly evolve directly from the tar given off from the devolatilization. This is based on drop tube measurements of coal devolatilization in an argon atmosphere that indicate that the sum of soot and tar are relatively constant (McLean et al., 1980 and Seeker et al., 1980). Similar to gas-derived soot, coal soot then undergoes oxidation, surface growth and agglomeration.
Recently, Adams and Smith (1995) developed a simple empirical model for turbulent soot formation that related the soot volume fraction to the local equivalence ratio. Soot was assumed to exist where the local equivalence ratio was 1.0 and above, increasing linearly to a maximum value at an equivalence ratio of 2.0 and above. The maximum soot value was calculated as a direct function of the amount of volatile carbon calculated to exist at that point. The soot volume fraction was then related to the radiative properties using Equation 4. They concluded that the inclusion of a soot radiation model increases predicted radiative transfer, however the maximum local temperature difference between predictions with and without the soot model was lower than expected (about 50 K). Ahluwalia and Im (1994) developed a similar model, and reported that soot significantly enhanced the radiative heat transfer. Both models use an empirical survivability constant of 0.1, which serves to reduce the predicted soot concentrations.
Frenklach (1992) also developed a model for hydrocarbon flames using detailed kinetics to determine soot formation. He reported a mechanism with 337 reactions and 70 species. Leung et al. (1991) similarly developed a more simplified kinetics model with 111 reactions. While full kinetic mechanisms can be quite accurate, these methods are computationally intensive, and this puts them outside the scope of current comprehensive modeling codes.
Kennedy, et al. (1990) developed a more complex relationship for axi-symmetric laminar gas diffusion flames using the transport differential equations for the volume fraction, adding in nucleation, surface growth, and oxidation source terms. Other researchers have recently used variations of this relationship by solving transport equations for nucleation and mass fraction of soot, which may be related to the volume fraction by assuming an average density. This involves the derivation of their own estimates for the nucleation, surface growth, and oxidation terms (Honnery and Kent, 1992, Sivathanu and Gore, 1994). In a study by Coelho and Carvalho (1994), two different soot formation models were coupled with three different oxidation models taken from different researchers in an effort to determine which models correspond the best to measured data. They were added to predictive codes and solved with the transport equations for the number densities and concentrations of soot.
Comparisons were made regarding the predictions of soot in a turbulent propane diffusion flame between the various combinations of models and measured data. Recently, this method has been applied to a turbulent 3-dimensional flame (Fairweather et al., 1992). In all of these studies, reasonable agreement existed between measured soot volume fractions and predicted ones. These studies have been applied to gas flames only, and therefore assume that the soot forms from acetylene.
Approach
This research extends the approach of Kennedy, et al. (1990) to coal-derived soot by generating the proper conservation equations, source terms, and boundary conditions for 3-dimensional calculation of soot and tar mass fraction (Ys and Yt respectively). The basic pathway considered for soot formation from coal is illustrated in Figure 2. The boundary conditions for soot and tar are similar to the boundary conditions for other flowfield variables such as the coal gas mixture fraction (eta) and the mixture fraction variances (g). References are available for more information (PCGC-3 Users Manual, 1993; Smoot and Smith, 1985). The equations for conservation of mass are as follows:
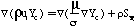
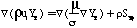
Where mu is the viscosity, sigma is the Schmidt number, rho is the time-averaged density, and u is the ith component of Favre averaged velocity. S represents the source terms for the equations:
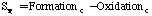
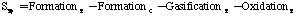
where:
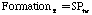
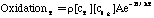
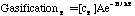
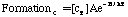
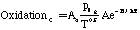
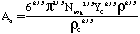
Where SP is the tar mass source term computed in the particle phase calculations, T is the gas temperature, [c] is the mass fraction of tar or oxidant, A is the pre-exponential factor, E is the activation energy, R is the gas constant, pO2 is the partial pressure of oxygen, (C is the average density of soot (assumed to be 1950 kg/m3), and Navg is the average number density assumed to be 1.0E16 m-3 (Kennedy et al., 1990). Table 1 gives a description of the Arrhenius constants used, along with the source.
| Term | A | E (kJ/g-mol) | Source |
|---|---|---|---|
| FormationT | N/A | N/A | Particle Phase Calculations |
| OxidationT | Variable | Variable | Shaw et al. (1990) |
| GasificationT | 9.77E10 (1/s) | 286.9 | Ma (1996) |
| FormationC | 5.02E8 (1/s) | 198.9 | Ma (1996) |
| OxidationC | 1.09E4 (K^0.5/s) | 164.5 | Lee et al. (1962) |
| Ao | N/A | N/A | Kennedy et al. (1990) |
Once the value of YC has been calculated from Equation 6, the volume fraction may be calculated using the following equation:

The absorption coefficient may then be determined using Equation 3. This absorption coefficient is then summed with the calculated absorption coefficient for the radiating gases (i.e., CO2 and H2O) to form a total absorption coefficient.
Method
In order to validate the model, predictions are compared with measured values of soot yield, gas temperature, and NOx concentration from three models. It is expected that the model will give reasonable soot yields, and that NOx and temperature predictions will better conform with measured values. The model of Adams and Smith (1995) has also been coded for comparison purposes.
Flat Flame Burner
The Flat Flame Burner (FFB) is a laminar flow reactor at BYU. Premixed fuel-rich methane and air are uniformly injected through a 5cm x 5cm honeycomb grid. The gases ignite, forming a uniform, thin flame sheet. Coal particles are injected through a narrow 3mm diameter tube in the center of the burner slightly above the tip of the flame sheet (Figure 3). The hot product gases cause the coal to devolatilize without the occurrence of oxidation. A suction probe is placed above the flame, which collects the char and soot. The char and soot may be separated aerodynamically using a virtual impactor and cyclone system. Total soot yields were measured as a function of the height of the probe above the burner surface by Ma (1996). These data include measured temperature profiles at various heights and axial positions, char and soot yields from the coal at various heights, and particle and gas velocity measurements at various locations. This apparatus was modeled with a 25x25x28 grid using PCGC-3, assuming laminar flow. The case modeled was the Pittsburgh #8 coal at 1800 K.
Controlled Profile Reactor
The Controlled Profile Reactor (CPR) is a test scale furnace that was designed specifically to measure coal flame parameters. The reactor is axi-symmetric, which allows 2-dimensional model predictions (Figure 4). The symmetry significantly reduces the computational requirements. Measurements of various gas species concentrations in the CPR have been documented by Sanderson (1993). Also, Butler (1992) measured particle and gas temperature profiles in the CPR, as well as heat fluxes at various locations. This research has modeled Case 5 from these sources using a 75x51x3 grid (2 planes are symmetry planes). This lean case included a secondary swirl of 1.4, coal flow rate of 11.4 kg/hr, mass-mean particle size of 55 micro m, primary air flow rate at 289 K of 15 kg/hr, and secondary air flow rate at 533 K of 127 kg/hr. The fuel used was Utah Blind Canyon hvB bituminous coal.
Fireside Performance Test Facility
The ABB/CE Fireside Performance Test Facility (Figure 5) is a cylindrical scale furnace which was also used to make gas species concentration and temperature measurements (Thornock et al., 1993). Test 5, a lean (phi = 0.83) Ashland (West Virginia) hvA bituminous coal flame, was modeled using a 69x57x44 grid. The mass mean particle size was 41.9 micro m, coal feed rate was 118 kg/hr, primary air rate was 100kg/hr, and secondary air feed rate was 1360 kg/hr.
Results
The purpose for using the FFB model was to have a means with which to compare the soot model to actual measurements of soot. Figure 6 shows good comparison between measured and predicted soot yields for this case. Additionally, once the tar is gone, the model predicts that the soot yield is relatively constant. Because the soot volume fraction is low, the radiative contribution and consequently the temperature difference between the model predictions with and without the soot model is negligible. It should be noted that the Adams (1995) model does not work for this case because the model calculates the soot as a function of the equivalence ratio. Since the methane contributes significantly to the calculated equivalence ratio, the Adams (1995) model would overpredict the soot: it would treat the methane as if it had the same sooting potential as did the coal.
Figures 7 and 8 show temperature profiles in the CPR at two different heights, one near the burner and the other further down stream. The predictions without soot for the most part are higher than the measured values. Upon considering soot, the predicted temperature values become closer to the measured values. This is consistent with what was expected to occur upon the addition of the soot radiation model. This serves to qualitatively validate the model. However, the absolute agreement with measured temperatures is still in need of improvement. While the Adams (1995) soot model generally predicts lower temperatures than the model without soot, the new model developed for this research predicts temperatures to be even lower. This is a result of higher predicted soot volume fractions in the new model than in the Adams (1995) model.
Figures 9 and 10 show temperature and NOx profiles for the FPTF case respectively. The data shown occur far down-stream in the reactor. The difference between the Adams (1995) model and the code without soot for both NOx and temperature predictions appears to be minimal. The new soot model in both cases compares more closely to the measurements. This would indicate based on the comparison of FPTF measurements to predictions, the new soot model allows the code (PCGC-3) to more accurately model combustion flames.
Discussion
The new model presented here uses the CPD model to determine tar and total volatiles yields; input to the CPD model come directly from 13C NMR measurements of the structure of the parent coal. The tar yield is then directly used in the reaction scheme to determine soot yield, and therefore no empirical constants are needed beyond the reaction rate parameters, which were taken from the experimental data of Ma (1996) and seem to be independent of coal type. Therefore, this model avoids the empirical "survivability" constant used in previous models.
The predictions with the soot model presented here indicate that (a) the soot radiation seems to lower temperatures in the flame zone, and (b) that the predicted temperatures lie closer to measured data than the predictions without the soot model. Additional work must be done to further quantify the effect of soot radiation, most notably the interaction between the soot radiation and turbulence. The effects of turbulence on the tar-soot reactions must also be considered. It may also be necessary to include an additional conservation equation for soot particle number density (Fairweather et al., 1992) and rate to account for the effects of soot oxidation by OH radicals (Puri et al., 1994).
Summary and Conclusion
A model for soot formation from coal tar was developed based on measurements of coal-derived soot yields in a laminar flow reactor. The model assumes that coal tar can either form soot, oxidize or be gasified to light gas prior to combustion. The soot model was incorporated into a comprehensive coal combustion code (PCGC-3), which uses the CPD model to predict local tar concentration from the chemical structure data on parent coals. Rates for the soot formation were taken from experimental data, and found to be independent of coal type. The resulting model eliminates the need for empirical "survivability" constants found in previous models.
Comprehensive model predictions were made with and without the soot model for three reactors, ranging from lightly loaded laminar flow reactor experiments to small pilot scale furnaces where temperature measurements were available. Prediction of the laminar flow reactor matched measured gas temperatures and soot yields. Results in the larger furnaces indicated the importance of soot radiation in the prediction of local gas temperatures near and just after the burners, and hence NOx concentrations.

Figure 1. A Comparison of Two Soot Emissivity Models (Le=1.0m).

Figure 2. Presumed Pathways for the Formation of Coal Derived Soot (Ma, 1996).
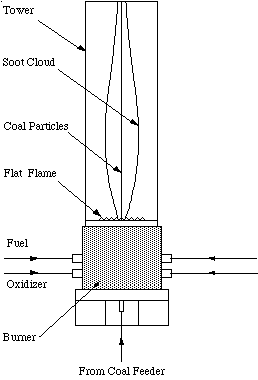
Figure 3. A Drawing of the Flat Flame Burner at BYU.
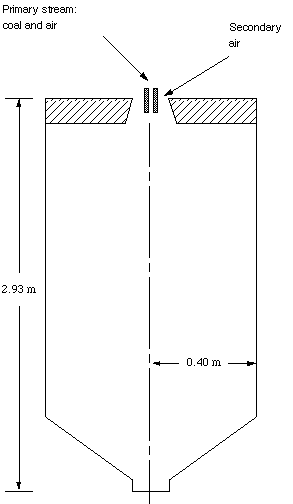
Figure 4. A Drawing of the Controlled Profile Reactor at BYU.
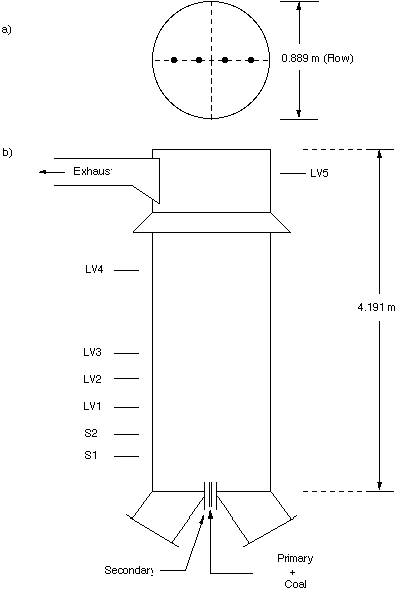
Figure 5. A Drawing of the ABB/CE Fireside Performance Test Facility.
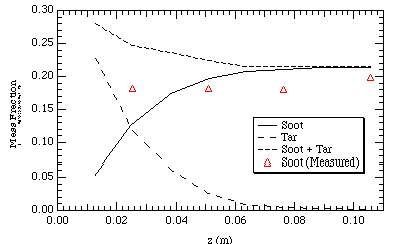
Figure 6. FFB model yields compared with measurements.
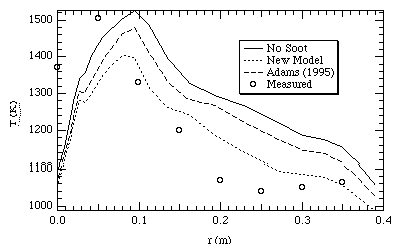
Figure 7. CPR temperatures at 30 cm below the inlet.
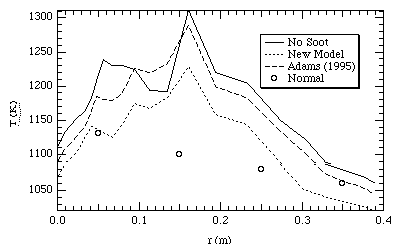
Figure 8. CPR temperatures at 150 cm below the inlet.
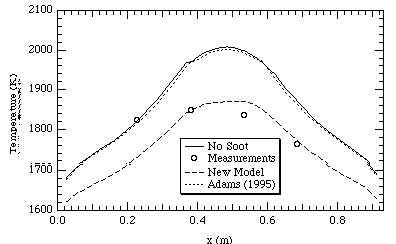
Figure 9. FPTF temperatures at 2.6 m above the inlet.
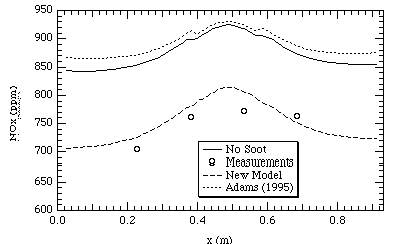
Figure 10. FPTF NOx at 2.6 m above the inlet.
References
Adams, B. R., "Computational Evaluation of Mechanisms Affecting Radiation in Gas-and Coal-Fired Industrial Furnaces," Ph.D. Dissertation University of Utah (1993).
Adams, B. R., and P. J. Smith, "Modeling Effects of Soot and Turbulence-Radiation Coupling on Radiative Transfer in Turbulent gaseous Combustion," Combustion Science and Technology, 109, 121-140 (1995).
Ahluwalia, R. K. and K. H. Im, "Spectral Radiative Heat-Transfer in Coal Furnaces using a Hybrid Technique", Journal of the Institute of Energy, 67, 23-29, March (1994).
Butler, B. W., "An Experimental Evaluation of Radiant Energy Transport in Particle- Laden Flames," Ph.D. Dissertation, Brigham Young University (1992).
Coelho, P. J., and M. G. Carvalho, "Modeling of Soot Formation in Turbulent Diffusion Flames." ASME paper, HTD-Vol. 272, Heat Transfer in Fire and Combustion Systems (1994).
Fairweather, M., W. P. Jones and R. P. Lindstedt, "Predictions of Radiative Transfer from a Turbulent Reacting Jet in a Cross-Wind," Combustion and Flame, 89, 45-63 (1992).
Fletcher, T. H., A. R. Kerstein, R. J. Pugmire, M. S. Solum and D. M. Grant, "Chemical Percolation Model for Devolatilization. 3. Direct Uses of C NMR Data To Predict Effects of Coal Type," Energy & Fuels, 6, 4, 414-431 (1992).
Frenklach, M., "Development of Predictive Reaction Models of Soot Formation", Annual Technical Report, Grant No. AFOSR 91-0129, January 31, (1991).
Honnery, D. R., and J. H. Kent, "Soot Mass Growth Modeling in Laminar Diffusion Flames." Twenty-Fourth Symposium (International) on Combustion/The Combustion Institute, 1041-1047 (1992).
Hottel, H. C. and A. F. Sarofim, Radiative Transfer, McGraw-Hill, New York (1967).
Kennedy, I .M., W. Kollmann and J. Y. Chen, "A Model for Soot Formation in a Laminar Diffusion Flame," Combustion and Flame, 73-85, July (1990).
Kent, J. H., and D. R. Honnery, "A Soot Formation Map for a Laminar Ethylene Diffusion Flame," Combustion and Flame, 79, 287-298 (1990).
Kollmann, W., I. M. Kennedy, M. Metternich and J.-Y. Chen, "Application of a Soot Model to a Turbulent Ethylene Diffusion Flame," Springer Series in Chemical Physics, 59, 503-526 (1994).
Lee, K. B., M. W. Thring and J. M. Beer, "On the Rate of Combustion of Soot in a Laminar Soot Flame," Combustion and Flame, 6, 3, Sep. (1962).
Leung, K. M., P. Lindstedt and W. P. Jones, "A Simplified Reaction Mechanism for Soot Formation in Nonpremixed Flames," Combustion and Flame, 87, 289-305 (1991).
Ma J., "Soot Formation and Secondary Reactions During Coal Pyrolysis," Ph.D. Dissertation, Brigham Young University (1996).
Majidi, V., N. Xu and K. Saito "Probing Soot Particles Using Laser Based Techniques," SPIE 2122, 146-152 (1994).
McLean, W. J., D. R. Hardesty, and J. H. Pohl, "Direct Observations of Devolatilizing Pulverized Coal Particles in a Combustion Environment," Eighteenth Symposium (International) on Combustion, 1239 (1980).
Menguc, P. C. and B. W. Webb, "Radiative Heat Transfer." Chapter 5 Fundamentals of Coal Combustion for Clean and Efficient Use, edited by Smoot, L. D., 375- 431 (1993).
Nenniger, R. D., J. B. Howard and A. F. Sarofim, "Sooting Potential of Coals," Proceedings of the 1983 International Conference on Coal Science, 521 (1983).
PCGC-3 Users Manual, Published by the Advanced Combustion Engineering Research Center, Brigham Young University (1993).
Puri, R., R. J. Santoro, and K. C. Smyth, "The Oxidation of Soot and Carbon Monoxide in Hydrocarbon Diffusion Flames," Combustion and Flame, 97, 125-144 (1994).
Rigby, J. "Experimentally Determined Optical Properties, Volume Fraction and Temperature Measurements of Coal Soot in a Slot Flame Reactor," Ph.D. Dissertation, Brigham Young University (1996).
Sanderson, D. K., "Composition of Combustion Gases and Particles in a Pulverized Coal- Fired Reactor," M. S. Thesis, Brigham Young University (1993).
Seeker, W. R., G. S. Samuelson, M. P. Heap, and J. D. Trolinger, "Thermal Decomposition of Pulverized Coal Particles," Eighteenth Symposium (International) on Combusion, 1213 (1980).
Shaw, D. W., X. Zhu, M. K. Misra, and R. H. Essenhigh, "Determination of Global Kinetics of Coal Volatiles Combustion," Twenty-Third Symposium (International) on Combustion, 1155-1162 (1990).
Siegel, R. and J. R. Howell, Thermal Radiation Heat Transfer Third Edition, Hemisphere Publishing Corporation (1992).
Sivathanu, Y. R., and J. P. Gore, "Coupled Radiation and Soot Kinetics Calculations in Laminar Acetylene/Air Diffusion Flames." Combustion and Flame, 97, November, 161-172 (1994).
Smoot, L. D. and P. J. Smith, Coal Combustion and Gasification, Plenum Press (1985).
Thornock, D. E., P. J. Grandia, and B. F. Griffith, "Combustion Modeling: A Combustion Data Set Taken in the Pilot-Scale Fireside Performance Test Facility", Company Confidential, ABB Power Plant Laboratories, 5, March (1993).
Villasenor, R., and I. M. Kennedy, "Soot Formation and Oxidation in Laminar Diffusion Flames," Twenty-Fourth Symposium (International) on Combustion, 1023- 1030 (1992).
Dr. Fletcher home page
, ACERC home page
, BYU ChE Dept home page
, BYU home page