¹³C NMR spectroscopy has been shown to be an important tool in the characterization of coal structure. Important quantitative information about the carbon skeletal structure is obtained through ¹³C NMR spectral analysis of coal. Solid-state ¹³C NMR analysis techniques have progressed beyond the mere determination of aromaticity, and can now describe features such as the number of aromatic carbons per cluster and the number of attachments per aromatic cluster. These ¹³C NMR data have been used to better understand the complicated structure of coal, to compare structural differences in coal, tar, and char, and to model coal devolatilization.

Unfortunately, due to the expense of the process, extensive ¹³C NMR data are not available for most coals. A non-linear correlation was therefore developed that predicts the chemical structure parameters of both U.S. and non-U.S. coals generally measured by ¹³C NMR and often required for advanced devolatilization models. The chemical structure parameters correlated include: (i) the average molecular weight per side chain (M_d); (ii) the average molecular weight per aromatic cluster (M_cl); (iii) the ratio of bridges to total attachments (p₀); and (iv) the total attachments per cluster (s+1). The correlation is based on ultimate and proximate analysis, which are generally known for most coals. ¹³C NMR data from 30 coals were used to develop this correlation. The correlation was used to estimate the chemical structure parameters generally obtained from ¹³C NMR measurements, and then applied to coal devolatilization predictions using the CPD model. It will be shown that the predicted yields compare well with measured yields for most coals. A detailed description of the correlation is given by Genetti¹

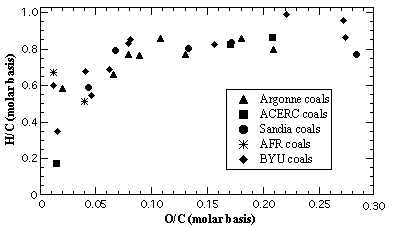
A database of 30 coals was used in this study, including the ultimate analysis and the four chemical structure parameters derived from ¹³C NMR analysis. Eight of the coals were Argonne premium coals, three were studied at the Advanced Combustion Engineering Research Center (ACERC), five coals were studied at Sandia National Laboratories (selected from the Penn State Coal Bank), two were studied at Advanced Fuel Research, and twelve coals were selected from the Penn State Coal Bank to expand the database for this study. The 30 coals that make up the database vary widely in rank as shown in the coalification chart in Figure 1.

Figure 1. Coalification chart of 30 coals used in this research showing the diversity of rank of the selected coals.

As a first step, each of the ¹³C NMR parameters was plotted versus each independent variable (i.e. elemental composition and ASTM volatile matter content). This permitted a first order screening to determine the relative dependence on each independent variable, and allowed a visual inspection of correlation patterns. Secondly, a separate non-linear (i.e., a polynomial) correlation was made for each independent variable, and a pseudo r2 value was calculated to determine the strength of each correlation. A variety of equation forms were examined, and experience showed that a cubic polynomial generally resulted in the best fit for most parameters. Finally, from the individual polynomial correlations, the form of the correlation was derived between each ¹³C NMR parameter and the combination of all of the independent variables.

p0 was plotted versus each independent variable (i.e. elemental composition). From these plots it was seen that the value of p0 depends significantly on the relative content of carbon (X_C), hydrogen (X_H), oxygen (X_O), and ASTM volatile matter content (X_VM). Once it was determined that p0 was dependent on the carbon, hydrogen, oxygen, and ASTM volatile matter content, the forms of the "best fit" equations from the four plots (p0 versus X_C, p0 versus X_H, etc.) were added together, resulting in the following equation:

p₀ = c₁ + c₂X_C + c₃X_C² + c₄X_c³ + c₅X_H + c₆X_H² + c₇X_H³ + c₈X_O + c₉X_O² + c₁₀X_O³ + c₁₁X_VM + c₁₂X_VM² + c₁₃X_VM³

where the c_i are empirical coefficients, and the elemental composition and ASTM volatile matter content are on a dry ash free basis. All of the "best fit" equations were third order polynomials which resulted in the modified cubic correlation. Initial guesses for the coefficients were usually a value of 1 or 0. The sum square error between the measured value and the predicted value of p₀ was minimized by optimizing the coefficients. This procedure was repeated for M_d, M_cl, and s+1, resulting in similar equations. Through this study it was determined that the chemical structural parameters have little dependence on the relative content of sulfur and nitrogen. Therefore, sulfur and nitrogen were omitted from the correlations.

During the course of this research, while applying this modified cubic correlation to additional sets of NMR data for other coals, it was found that unrealistic values for M_cl and s+1 were obtained for low rank coals (X_O > 0.25) and high rank coals (VM < 0.10). For example, some predicted values of M_cl were less than 100 daltons; the lowest NMR measurement for any coal was ~200 daltons. These unrealistic predicted values seemed to be the result of extrapolations of the cubic curve beyond the original data set. Therefore, the curve-fitting procedure was repeated for a quadratic set of equations, as shown below:

p₀ = c₁ + c₂X_C + c₃X_C² + c₄X_H + c₅X_H² + c₆X_O+ c₇X_O² + c₈X_VM + c₉X_VM²

where y = Md , M_cl, s+1, and p0. By using the quadratic correlation rather than the cubic, the number of coefficients were reduced, with a small corresponding penalty in the value of r². The extrapolated values of the quadratic correlation seemed more reasonable for low and high rank coals.

To further improve the correlations, NCSS² (Number Cruncher Statistical Software) was used to examine the data set for outliers and cross-correlations. A factor analysis was performed to determine the optimum number of independent variables to be used in each correlation. Based on this analysis, it was determined that Equation 2 is a suitable correlation.

The non-linear curve fitting package in NCSS was used to determine the coefficients corresponding to each equation. NCSS estimates the parameters of the non-linear models using the Levenberg-Marquardt non-linear least squares algorithm.³

The coefficients of determination, r²,were 0.94, 0.72, 0.88, and 0.62 for the quadratic correlations of Md, M_cl, p0 and, s+1, respectively. There is no direct r² defined for non-linear regression. The r² value calculated by NCSS and reported here is a pseudo r² value constructed to approximate the r² value used in multiple regression. The version of r² used for non-linear regression indicates how well the model performs after removing the influence of the mean of the dependent variable. For example, an r² value of 0.72 for M_cl means that approximately 72% of the variance of M_cl can be explained by the non-linear relationship between M_cl and the independent variables (i.e. elemental composition and ASTM volatile matter content). Only about 62%, however, of the variance of s+1 is explained by the correlation.

Each of the three devolatilization models mentioned previously require an estimation of the number of stable bridges existing in the parent coal or that are formed early in the pyrolysis process for low rank coals. In the CPD model, this parameter is c₀. This parameter has generally been used to represent stable bi-aryl type linkages in low volatile bituminous coals, and to represent early crosslinking in lignites. In the past, c₀ has been used as a tuning parameter for these types of coals, and had to be changed as a function of heating rate, since crosslinking occurs at different rates as a function of heating rate. Based on drop tube and flat flame burner pyrolysis experiments performed by Watt⁴ at heating rates greater than 10⁴ K/s, and pyrolysis experiments conducted by Fletcher and Hardesty⁵ at Sandia National Laboratories, a rough correlation for c₀ was developed. For low rank coals, oxygen content in the parent coal was used, since this correlates well with early crosslinking. For high rank coals, carbon content was used, since this may correlate well with the bi-aryl type linkages. The correlation for c₀ used for high heating rates was:

c₀ = min[0.36, max{(0.118 X_C - 10.1), 0.0}]+ min[0.15, max{(0.014 X_O - 0.175), 0.0}]

where X_C and X_O are the percent carbon and oxygen, respectively, on a dry as free basis. Equation 3 was used in the CPD model for all predictions that used the correlated (and measured) chemical structure parameters.

Two sets of test cases were used to evaluate the reliability of using correlated structural parameters in the CPD model to predict total volatiles and tar yields. The first test case was a series of flat flame burner devolatilization experiments reported by Fletcher and Hardesty.⁵ Predictions were made by the CPD model using (a) the actual NMR structural parameters and (b) the structural parameters estimated by the correlations. The five coals used in this test case were part of the database used in the correlations. Predictions are compared with measurements in Figure 2. It can be seen that the use of the estimated structural parameters from the correlation gives predictions of total mass release that are as good as the actual NMR data in most cases. The average relative error between the predicted total volatiles yield and the measured total volatiles yield was 6.8% using the actual NMR structural parameters and 3.8% using the correlated parameters. For this set of test cases, using the correlated NMR parameters instead of the measured NMR parameters actually resulted in more accurate predictions of total mass release. It is anticipated, however, that for some unusual coals actual structural parameters derived from actual ¹³C NMR analysis will be needed to achieve accurate predictions of volatiles yields by the CPD model.

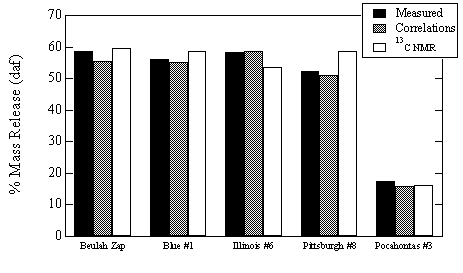
Figure 2. Comparison of CPD predictions with measured total mass release. The measured values refer to flat flame burner experiments conducted at Sandia, NMR values refer to CPD predictions of mass release using actual NMR structural parameters, and the correlation values correspond to CPD predictions of mass release using the correlated structural parameters.

The second set of test cases consisted of total volatiles and tar yields for 17 coals used in devolatilization experiments by Xu and Tomita.⁶ Xu and Tomita used a Curie-point pyrolyser to heat samples at 3000 K/s to 1037 K with a 4 second residence time at that temperature. NMR data are not available for this set of coals. None of the structural parameters estimated by the correlations seem unreasonable (e.g., values of M_cl fell within known limits for all coals studied). Figure 3 shows the predicted and measured mass and tar release versus percent carbon in the parent coal. The predicted mass release and tar yields compare well with the values and trends of the corresponding measured yields for most of the coals tested. Average relative errors between the predicted values and the measured values were 13% for mass release and 20% for tar release. Overall, there does not appear to be a positive or negative bias in the error.

The CPD model, however, over-predicted total mass release for coals in the range of 80 % to 84 % dry-ash free carbon content (Hunter Valley, Liddell, Newvale). The mass release measured by Xu and Tomita for the coals in this range seem low compared to total volatiles yields measured by other investigators for similar coals and similar conditions.^4,5,7-9 This suggests that the Hunter Valley, Liddel, and Newvale samples are particularly unusual coals, or there was some error in the experimental determination of the total volatiles yields for these coals in the study conducted by Xu and Tomita. Recently, an investigator conducted a pyrolysis experiment on a Hunter Valley coal at conditions similar to those used by Xu and Tomita, and measured a total volatiles yield of 48% (daf).¹⁰

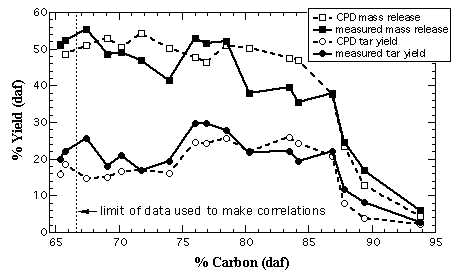
Figure 3. Comparison of CPD predictions with measured total mass release and tar yields. The measured values refer to the Curie-point pyrolyser experiments performed by Xu and Tomita.⁶ CPD mass release and CPD tar yield refer to the CPD predictions using structural parameters estimated by the correlations developed in this research. The dotted line at 66.6 % C (daf) shows the lower boundary of the original data set. The upper bound is 95.4 % C (daf).

Non-linear correlations were developed to model the average structural characteristics of coal as a function of elemental composition and ASTM volatile matter content. The coefficient of determination, r², is a measure of how well the correlation explains the variation in the dependent variable as a function of the independent variables. The r² values for these correlations were 0.94, 0.72, 0.88. and 0.62 for Md, M_cl, p0, and s+1,respectively. Reasonable estimations of ¹³C NMR structural parameters for most coals can be expected using the correlation. However, it is expected that these correlations, just like any correlation, will not work well for some unusual coals.

The non-linear modified quadratic correlation of ¹³C NMR measurements of coal structure with ultimate analysis and volatile matter content seems to be an appropriate method to estimate the coal structure input parameters for network devolatilization models, such as the CPD model. The correlation, combined with the CPD model, appears to work well in predicting total volatiles and tar yields for low to high rank coals. Although one of the principal motives for this study has been the estimation of the input parameters for the CPD model, the estimated structural parameters should be useful in other applications, and a similar approach could be used to develop predictive models for other structural parameters.

Return to calculator