ChEn 273 Homework Hints

2.6 - Please use $3.00/gal instead of the $1.25/gal.

2.11 - The mass is equal to the density times the volume. The volume is equal to the height times the cross sectional area. If you set up an equation where the mass of the entire object is equal to the mass of the displaced fluid, the cross-section area cancels out because it appears on both sides of the equation.

2-31 - Note that the problems in the workbook are different than the problems in the textbook. I think the problems in the workbook make it look confusing. Please work the problems in the book.

2-38 - Please work part (a) algebraically by hand, as outlined on page 2-13 in the workbook. Work part (b) using the Solver in Excel using all of the data. Compare predictions of Z using the two correlations.

3-18 - The word suspension means the slurry, or the combination of liquid and solid.

3-23.

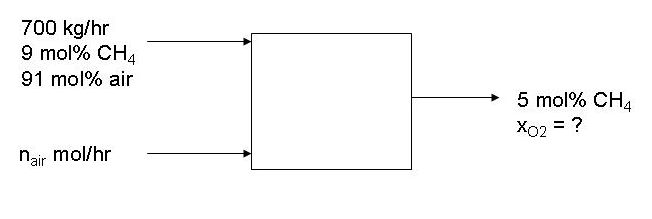
a. Find average MW of stream 1.
b. Find molar flow rates of air and CH4 in stream 1.
c. Find molar flow rate of second air stream that makes 5 mol% CH4 in output stream. You should use an equation like 0.05 = n_CH4/(n_CH4 + n_air1 + n_air2).
d. Find mass fraction of O2 in outlet stream from molar fow rates.

3-48 – (a) Use 65 deg F; (b) use -30 deg C; (c) start with a delta T of 40 K; (d) start with a delta T of 40 deg R.

4-13c. Try performing a balance around the purifier to see if the mass of P entering the purifier is equal to your calculated mass of P coming out of the purifier.

4-17.

4-28. The only thing required on this problem is to set up the degree of freedom analysis. No calculations are required!

4-29. Only solve for the requested values. The answer for the toluene recovered should be 89%.

4-42. For the first part, assume a basis of 100 mols of product, then do element balances. Scaling can then be done for the last part.

4-50. On part (c), please do the algebra by hand. It is pretty easy.

4-51. Read footnote on DOF for this problem. It is pretty rare that the element balances are independent, but it happens here. Prove that 2*(C balance) + 2*(O balance) = H balance. I found a spreadsheet to be useful for this problem.

4-59. Instead of EZ-Solve to solve 5 equations and 5 unknowns, try working this (a) by hand (not too hard), and (b) by Mathcad or Excel using a solver routine.

4-70. Please use a spreadsheet for part (c) so you do not have to fill in the calculations on page 4-43 in the workbook.

6-9. Please work this problem with both the Antoine equation and the DIPPR database.

6-33. Both mass fractions and mol fractions are used in this problem. Mole fractions are calculated from the vapor pressures, so it will likey be easier to solve the dry air and the water balances by mole fraction. The volumetric flow rate of "air" asked for in the problem is the flow rate of wet air. On the last part, you will have to do balances on water and on dry air to get 2 equations and 2 unknowns.

6-61. This problem is intended to make you think about whether the gas mole fraction is known or the liquid mole fraction is known, and how this relates to dew point and bubble point calculations. Please make this connection in your mind. Note that the "overhead product" is the vapor stream leaving the condenser.

(a) partial condenser: To find the minimum pressure, you know the vapor composition and hence are performing a dew point pressure calculation (T = 40 deg C).

Total condenser: Since you know the liquid composition and are trying to prevent bubble formation, this is a bubble point pressure calculation at 40 deg C.

(b) This is just a simple balance on molar flow rates. You are given the overhead molar flow rate and the ratio of the reflux flow rate to the overhead flow rate.

(c) The molar flow rates are the same is in (b). You know the vapor composition, so you really are doing a dew point pressure calculation, which you already did in part (a). The liquid composition in the reflux stream is from Raoult’s law (everything known but xi). The composition of the feed stream is from a species mole balance on either species.

6-95. Once you find the compositions, you will have to do the species balances and total balance.

7-16. Since an equation is given for the enthalpy, you cannot use the steam tables. You may use the ideal gas law here to calculate the number of moles.

7-28. Assume that the total pressure is 1 bar.

7-41. You may assume that the total pressure is 1 bar or 1 atm (the workbook assumes 1 atm).

7-42b. You performed the overall energy balance in part (a). Remember that stream 2 is split into 2 equal parts; this should help you do the energy balance around the condenser. The overall Q is composed of the Q for the condenser and the Q for the reboiler.

8-74. The hardest part of this problem is the recycle. However, from an overall balance, you can see how much the inlet flow is reduced (by some factor), and hence you can adjust the heat flow, etc., by this same factor. The answer in the back of the book for 8.74b is correct for just the net heat from the air conditioning unit.

9-7c. Just write down the reaction and find the heat of reaction like on the other parts of the problem.

9-7d. The (c) phase means condensed, which should be interpreted as solid. Therefore you need the heat of melting as well to get the solid to a liquid.

9-32. This problem will go easier if you use an extent of reaction variable, so that the energy balance has only one unknown.

9-49. The only way to solve this problem is to assume that the H in the coal starts as H2(g). Please comment on how good of an assumption this really is. All C goes to CO2, N goes to N2, and all S goes to SO2.Get heat of reaction for each element going to products. Assume that all O ties up H in the form of H2O (liq).

9.54a. Don't forget to adjust the stoichiometry for the O in the methanol. Try assuming a basis of 100 moles of dry product gas. Remember that the dew point is when P_A = P*_A.

9.54b. The heat of vaporization applies at the boiling temperature. Don't forget to heat the liquid to the boiling temperature, then vaporize the liquid, then heat the vapor to 100 C.

9-65. I only want you to calculate the adiabatic flame temperature for this system as part (a). You do not have to derive a polynomial expression. For part (b), explain why this temperature is not accurate. In part (c), do the same calculation for air instead of pure O2 (i.e., 30% excess air).

14-6. Wow- This was a hard problem. The author's answer key had lots of mistakes. The solubilities are not in the book, but are listed in Perry's Chemical Engineering Handbook. To be consistent, let's use the following solubilities:
0.002 kg CaCO3/100 kg liquid H2O
0.003 kg CaSO3/100 kg liquid H2O
I found that sometimes drawing a unit separately, with the inlet and outlet streams, along with the different phases, helped me to sort through this problem. See the TA's to check answers.
On 14.6e, the second part of this problem is somewhat ambiguous.  What is really wanted is the mass fraction of each component in the wet solids.

14-7. I found it a lot easier to do this problem if I calculated the heat of formation of coal. The high heating value of the coal is given, which is the negative of the heat of combustion assuming that the hydrogen goes to liquid water. All reactants and products are 25 C for this value of the heat of combustion. Since the heat of combustion is the total enthalpy of the products minus the total enthalpy of the reactants, and the total enthalpies at 25 C are merely the weighted sums of the heats of formation, the only unknown in this equation is the heat of formation of coal. Assume a basis of 100 kg of dry coal, calculate the products, and then calculate the weighted sum of enthalpies, and finally determine the heat of formation of the coal.

14-10. The only way that this problem makes sense is if the heat input to the boiler is really the heating value of the coal going into the boiler. This is the way that the regulations are written.

14-14c. From the flow rate of methane, multiply the flow rate by the heat of combustion (i.e., the high heating value). This is an approximate heat addition rate. Then divide by the high heating value of the coal.