2.2.3-4 2e

Solve the following differential equation and sketch the solution curves:

subject to

Solution:

1^st order, non-linear, non-separable

homogeneous

1. Rewrite equation in standard differential form:

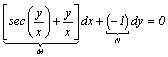
Change of variable:

separable

general solution

back substitution

use initial condition

solution of IVP

> implicitplot(ln(abs(exp(1)*x/2))=sin(y/x),

x=-3..3,y=-35..35,numpoints=100000);

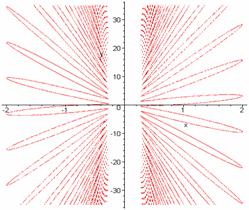
Note: Explicit solution narrows the integral curve:

> f:=x*arcsin(ln(abs(exp(1)*x/2)));

> plot(f,x=-3..3,y=-Pi..Pi,color=black);

2. Interesting form of solution can be obtained by converting equation to polar coordinates:

(solution has to be verified)

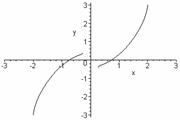
Integral curve is:

> c:=2/cos(arctan(Pi/2));

> polarplot(c*sin(tan(t))/cos(t),t=0..1.56,numpoints=1000);

if