10. Consider the differential equation:

a) find the general solution of the given ODE in the form of power series about the point ;

b) what is the radius of convergence of the obtained power series solution?

c) sketch the solution curves;

d) find the solution subject to the initial conditions: , .

Solution: It is already a solution, but it can be written

Solution:

b) Solution is convergent for any .

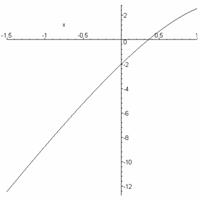
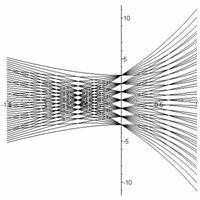
c) Plot the graph of solution curves:

d) Solution of IVP: