10. Consider the differential equation:

a) find the general solution of the given ODE in the form of power series about the point ;

b) what is the radius of convergence of the obtained power series solution?

c) sketch the solution curves;

d) find the solution subject to the initial conditions: , .

Solution: a)

is a singular point of given ODE (the only one).

is an ordinary point of given ODE. Therefore, two independent solutions can be found in the form (Theorem 2.10, p.163):

Differentiate it and substitute into equation

Use Identity Theorem (Theorem 2.6 p.160) – all coefficients in expansion are equal to zero:

recurrence formula for

Evaluate coefficients:

…

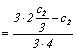
Write general solution:

It is already a solution, but it can be written

add and subtract

denote

recognize

Solution:

b) Solution is convergent for any .

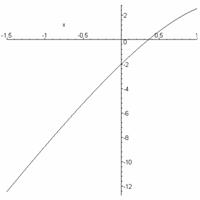
c) Plot the graph of solution curves:

d) Solve IVP:

Solution of IVP: