8i. Using the power series method, find complete solutions for the following differential equation

Solution:

is a singular point of given ODE (the only one). It is desired to find a power series

solution about this point because in this case solution will be convergent for any .

Check if the point is a regular singular point.

Rewrtite equation in normal form

Then

is analytic with

is analytic with

Construct indicial equation:

Let and , then (positive integer)

Consider case 2 of the Frobenius Theorem.

First solution can be found in the form:

Differentiate it and substitute into equation

recurrence formula for

Traditional function can be recognized.

For second solution use Reduction formula:

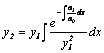
ALTERNATIVE Solution:

Look for solution with the second root of indicial equation (if we anticipate the presence of ):

Differentiate it and substitute into equation