8i. Using the power series method, find complete solutions for the following differential equation

Solution:

is a singular point of given ODE (the only one). It is desired to find a power series solution about this point because in this case solution will be convergent for any .

Check if the point is a regular singular point.

Rewrtite equation in normal form

Then

is analytic with

is analytic with

Construct indicial equation:

Let and , then (positive integer)

Consider case 2 of the Frobenius Theorem.

First solution can be found in the form:

Differentiate it and substitute into equation

divide by

Use Identity Theorem (Theorem 2.6 p.160) – all coefficients in expansion are equal to zero:

recurrence formula for

Evaluate coefficients:

…

Write general solution:

(see Theorem 2.5 4. p.159)

Second solution – Reduction formula:

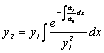
Therefore, absorbing coefficients by the arbitrary constants ,

The general solution can be written as

(see Section 5.6 Bessel Functions of half orders):

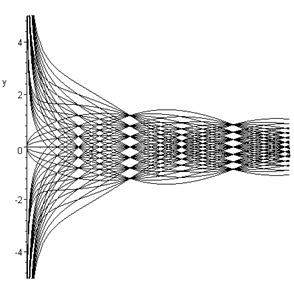
The graph of solution curves:

2.4-5 #8i

> restart;

General Solution:

> f:=c1/2*cos(x)/sqrt(x)+c2/2*sin(x)/sqrt(x);

Generate family of solution curves:

> f:={seq(seq(f,c1=-3..3),c2=-3..3)}:

> plot(f,x=0..4,y=-5..5,color=black);

ALTERNATIVE Solution:

Look for solution with the second root of indicial equation (if we anticipate the presence of ):

Differentiate it and substitute into equation

divide by

Use Identity Theorem (Theorem 2.6 p.160) – all coefficients in expansion are equal to zero:

recurrence formula for

Evaluate coefficients:

…

Write general solution: