#6

1) Find the solution of the Poisson Equation

in the domain subject to the boundary conditions:

, , ,

2) Sketch the graph of the solution for , and

a) ,

b) ,

Feel free to modify the conditions, if you think that it improves the problem.

Solution:

I Non-homogeneous equation with 2 homogeneous and 2 non-homogeneous boundary conditions.

Use the superposition principle to reduce the problem to set of basic problems (4.6.2 7-8, pp. 284-285):

1)

in the domain subject to the boundary conditions:

, , ,

2)

in the domain subject to the boundary conditions:

, , ,

3)

in the domain subject to the boundary conditions:

, , ,

Then the total solution will be:

II Solution of the basic problems:

1) Separation of variables:

Sturm-Liouville Problem (equation with two homogeneous b.c.):

Second equation:

Use shifted form of solution:

Apply

Therefore

Write the solution in the form of infinite series:

Apply the last b.c. to determine coefficients :

Treat it as the cosine Fourier series expansion of function , then coefficients are:

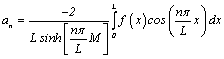
Then solution is:

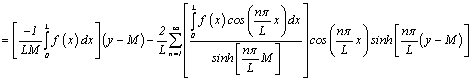
2) Separation of variables:

Sturm-Liouville Problem (equation with two homogeneous b.c.):

Second equation:

The solution:

Apply

Therefore

Write the solution in the form of infinite series:

Apply the last b.c. to determine coefficients :

Treat it as the sine Fourier series expansion of function , then coefficients are:

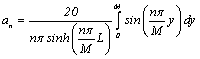
Then solution is:

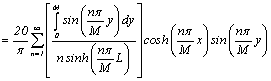
3) Poisson’s Equation

Sturm-Liouville Problem for X:

Sturm-Liouville Problem for Y:

Solution:

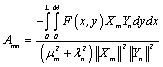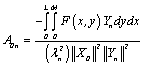
Then the solution is:

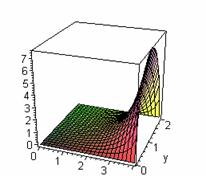
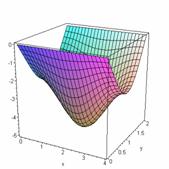
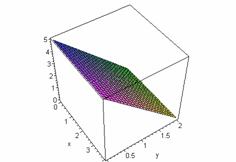
The graph of solution for the case a):

,

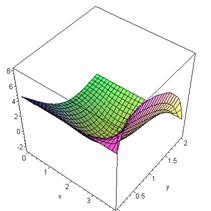
Solution for case b) see in the Maple example.