#16

a) Reduce the following BVP to Sturm-Liouville problem:

and find eigenvalues and eigenfunctions .

b) Use the obtained set of eigenfunctions for generalized Fourier series representation of the

function

in the interval

Sketch the graph for and .

Solution:

The 2^nd order ODE includes parameter.

We have to find the values of this parameter ()

for which ODE with boundary conditions has non-trivial solution .

The existence of such solution is provided by the Sturm-Liouville Theorem (4.5.3 p.268).

1) Reduce our BVP to SLP:

Rewrite equation in self-adjoint form with the help of the multiplication factor (4.5.4 Eq.19 p.271):

Identify coefficients

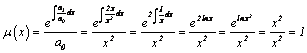
(self-adjoint form, Eq.5)

(operator form, Eq.13)

(both conditions are of the Dirichlet type)

According to Sturm-Liouville Theorem, this SLP has

infinitely many positive eigenvalues for which

boundary value problem has non-trivial solution (eigenfunctions).

2) Find eigenvalues and eigenfunctions (solve BVP)

2^nd order ODE, homogeneous, with variable coefficients, linear, Euler-Cauchy type

Auxiliary equation (see table “linear o.d.e.” Euler-Cauchy Equation):

case 1

general solution

apply boundary conditions:

Rewrite as a system in matrix form:

because

Therefore, system has only the trivial solution

which yields the trivial solution of BVP.

Therefore, there is no eigenvalues in the interval

case 2

general solution

apply boundary conditions:

It also yields the trivial solution.

case 3

general solution

apply boundary conditions:

non-trivial solution only if

eigenvalues

eigenfunctions

b) Generalized Fourier series expansion:

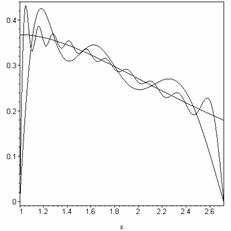
Maple example for :

> f:=x*exp(-x);

> u[n]:=sin(n*Pi*ln(x))/sqrt(x);

> N2[n]:=int(u[n]^2,x=1..exp(1));

> c[n]:=int(f*u[n],x=1..exp(1));

> f5:=sum(c[n]*u[n]/N2[n],n=1..5):

> f20:=sum(c[n]*u[n]/N2[n],n=1..20):

> plot({f,f5,f20},x=1..exp(1),axes=boxed,color=black);