5 c

Use Frobenius’ method to find the solution for the ODE

around the point .

Sketch the solution curves.

Solution:

1. Point is the only singular point of the ODE.

Check if it is regular singular point.

Rewrite equation in normal form:

analytic

analytic

Therefore, is a regular singular point.

Indicial equation

We have Case 2 of Frobenius’ Theorem:

2. The first solution can be found in the form:

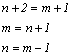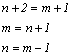
3. The second solution

multiply by

+

recurrence formula

choose then

Then the second solution becomes

4. Alternative solution for .

Because the second solution is in a simple closed form ,

we can use the reduction formula for obtaining

the other linear independent solution:

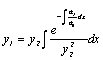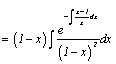
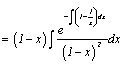
(integration with Maple)

Let us see if we can retrieve this solution from the power-series solution

We derived in the first part.

It is easy to check that both functions and

are solutions of the given ODE, but first function

duplicates the second solution.

So, the general solution of ODE can be written as

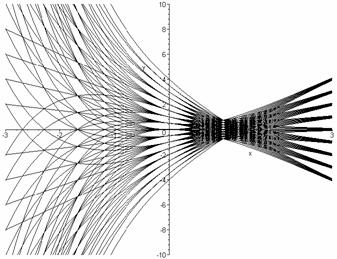
5. Solution curves

TEST #1 Problem 5c

Integration:

>

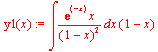
> f:={seq(seq(i/2*exp(-x)+j/2*(x-1),i=-4..4),j=-4..4)}:

> plot(f,x=-3..3,y=-10..10,color=black);