4.5.0
BANACH AND HILBERT SPACES
1.
Normed Space Norm is a map 
such that for all 
and 
1. 
if and only if 
2. 
3. 
(triangle
inequality)
Example:
in space 
of all continuous
functions in 
norm can be defined as
2.
Metric Space Vector
space 
is a metric space if there exists
a
function 
such that for all 
1. 
for
2. 
(symmetry)
3. for all 
(triangle
inequality)
is called the distance between .
Vector
space with introduced metric is called a metric space.
In the normed vector space the metric can be introduced as
3.
Inner Product Inner product is a map
such that for all
1. 
(
)
2. 
3. 
if and only if
Vector
space with introduced inner product is called an inner product
space. In inner product space the norm can be defined as
for all 
4. Convergence Let
be normed (metric space) and let 
, 
The
sequence 
converges to 
if
as 
The
sequence 
is called the Cauchy sequence (convergent in
itself) if
as and 
The
vector space is called complete if all its Cauchy sequences
are
convergent
in .
A complete normed space is called the Banach space. For example,
is a Banach space with
.
A complete inner product space is called a Hilbert space.
5. Orthogonality In the inner product space are called orthogonal if 
.
If
set 
consists
of mutually orthogonal vectors, 
when
, then this set is called an orthogonal set.
If
in addition, 
, then set is called
orthonormal.
Orthogonal set is linearly independent set.
If
set is
linearly independent then it can be converted to the
orthonormal
set 
with the
help of the so called Gram-Schmidt
orthogonalization process:
Gram-Schmidt process 
This algorithm can be formalized with the help of Gram’s determinant:
, 
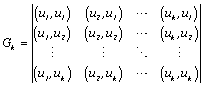Orthonormal vectors are detrmined by the formula
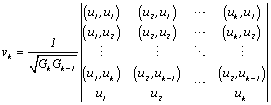
The
orthonormal set 
is said to be complete if there does not
exist
a vector 
, 
such that it is
orthogonal to all vectors
from
.
6. Fourier Series Let
be an orthonormal set.
is called the Fourier series (generalized
Fourier series)
are called the
Fourier coefficients, 
Theorem The Fourier series is convergent to the
function
if and
only if
(Parseval’s
equation)
Proof: Let 
■
Let
be an orthonormal set
.
If for any its Fourier series
converges
to 
in 
, then is said complete in .
7.
Vector Space 
Consider
a particular case of Equation 3.3 from Definition 3.13 (p.205),
with
and interval
:
Inner
product in vector space : For 
define:
inner product in 
weighted inner product in
with
the weight function 
Inner
product vector space belongs to the class of Hilbert spaces.
Introduced
inner product induces the norm in :
Historically, the first complete set was used by Fourier set of trigonometric functions
, 
in the interval 
.
The complete orthogonal sets used in the solution of PDE will be
generated by the solution of the Sturm-Liouville problems.
8. Exercizes: The
set of monoms 
is linearly
independent in 
.
a) Using the Gram-Schmidt orthogonalization algorithm with inner product
construct
an orthonormal set in
(the obtained set will be the set of the Legendre polynomials up the the scalar multiple).
b) Using the Gram-Schmidt orthogonalization algorithm with inner product
construct
an orthonormal set in
(the obtained set will be the set of the Tchebyshev polynomials up the the scalar multiple).
c) Use the obtained orthonormal sets for generalized Fourier series expansion of the function:
Compare
the results for truncated series with 2,3,4 terms. Make some observations.
The Scottish Cafe in Lvov
The original Szkocka Café (Scottish Café)
in
(on the left, shown at the time when it was
the Dessert Bar at Shevchenko Prospekt 27)
Now is a Bank (on the right).
The café was a
meeting place for many mathematicians including Banach, Steinhaus, Ulam, Mazur,
Kac, Schauder, Kaczmarz and others.
Problems were
written in a book kept by the landlord and often prizes were offered for their
solution.
A collection of these problems appeared later
as the Scottish Book.
R D Mauldin, The
Scottish Book, Mathematics from the Scottish Café (1981) contains the
problems as well as some solutions and commentaries.
