Laplace Equation (stationary heat transfer equation)

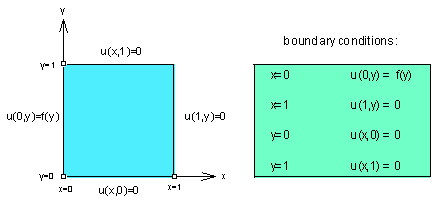
set of the problem ,

separation of variables we assume that function can be represented as a product of two functions each of single variable

substitute into heat equatio

in this equation, left hand side is a function of independent variable x only,

and right hand side is a function of independent variable y only.

The equality is possible only if both of them are equal to the same constant (call it ) .

Therefore,

it yields two ordinary differential equations:

and

solution of o.d.e. solution of o.d.e. depends on form of constant :

boundary conditions

start with

homogeneous b.c.

choose , then

therefore,

, where

, where

, where or

basic solutions:

b.c. for start with homogeneous boundary condition: (we already know that ), therefore the only solution

choose , then

but we know values of

where

basic solutions of LE

all these solutions satisfy LE and 3 homogeneous boundary conditions

and one boundary condition is left

any linear combination of basic solutions is also a solution

the idea is to find such combination that the last boundary condition is satisfied

so, we are looking for solution in the form

such that

at

non-homogeneous b.c.

let function be expanded in Fourier sine series

, where

after comparing it to solution at we can see, that if we take

then solution satisfies condition

solution of LE

particular case Let , then