3rd order linear ODE with constant coefficients      MapleFiles/ET502/ LODE3rdOrder.mws

>

restart;

>	with(linalg):

Warning, the protected names norm and trace have been redefined and unprotected

coefficients:

>	a0:=1;a1:=3;a2:=0;a3:=-4;

>	f:=exp(2*x);

auxilary equation:

>	ax:=a0*m^3+a1*m^2+a2*m+a3;

>	solve(ax=0,m);

fundamental set:

>	y1:=exp(-2*x);

>	y2:=x*exp(-2*x);

>	y3:=exp(x);

Wronskians:

>	A:=matrix(3,3,[y1,y2,y3,diff(y1,x),diff(y2,x),diff(y3,x),diff(y1,x$2),diff(y2,x$2),diff(y3,x$2)]);

>	A1:=matrix(2,2,[y2,y3,diff(y2,x),diff(y3,x)]);

>	A2:=matrix(2,2,[y1,y3,diff(y1,x),diff(y3,x)]);

>	A3:=matrix(2,2,[y1,y2,diff(y1,x),diff(y2,x)]);

>	W:=simplify(det(A));

>	W1:=factor(simplify(det(A1)));

>	W2:=factor(simplify(det(A2)));

>	W3:=factor(simplify(det(A3)));

Variation of parameter:

>	u1:=int(-W1/W*f/a0,x);

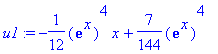
>	u2:=int(W2/W*f/a0,x);

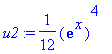
>	u3:=int(-W3/W*f/a0,x);

complimentary solution:

>	yc:=c[1]*y1+c[2]*y2+c[3]*y3;

particular solution of non-homogeneous equation:

>	yp:=u1*y1+u2*y2+u3*y3;

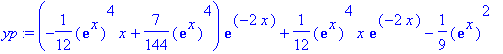
General solution of non-homogeneous equation:

>

y:=yc+yp;

>	y:=simplify(y);

>

Solution curves of homogeneous equation:

>	p:={seq(seq(seq(i*exp(-2*x)+j*x*exp(-2*x)+k*exp(x),k=-1..1),i=-1..1),j=-1..1)}:

>	plot(p,x=-1.5..2.5,color=black);

Solution curves of n0n-homogeneous equation:

>	p1:={seq(seq(seq(i*exp(-2*x)+j*x*exp(-2*x)+k*exp(x)+yp,k=-1..1),i=-1..1),j=-1..1)}:

>	plot(p1,x=-1.5..2.5,color=black);

>

>