Advanced Applied Engineering Mathematics
EngT 502/503
SCHEDULE WINTER 2006
CB 406 |
CB 406 |
CB 406 |
|||
CB 133 Vladimir |
CB 383 |
CB 133 Vladimir |
CB 383 |
CB 133 Vladimir |
|
CB 472 Reinhard |
CB 383 |
CB 472 Reinhard |
CB 383 |
CB 472 Reinhard |
| Some Topics from Linear Algebra | 3 
|
||
|
Ordinary Differential Equations |
Lecture Notes 2.1-2.5 (modified May 25, 2005) 
Lecture Notes 2.6 Systems of ODEs (modified May 20, 2005)
2nd order linear ODE with constant coefficients
3rd order linear ODE with constant coefficients
Euler-Cauchy Equation, example 4 (p.149)
Power Series Solution, example 2.11 (p.164)
Example of case 2 of Frobenius Theorem (TEST 1 #5c)
Systems of ODEs, example 4
Systems of ODEs with Maple, example 1
example 2 (autonomous system)
|
2.1: 10
2.2.1-2: 1a
1f
1g
2.2.3-4: 2e
3a
2.2.5: 1a
2.4-5: 1
8i
10
2.6: 4c
|
|
| Fourier Analysis |
Half and Quater Range Expansions
Gibb's Phenomena
Example 3.10
Example 3.12 (Unit Pulse)
|
||
|
Partial Differential Equations |
Lecture Notes (modified March 5, 2005)
4.5.0 Banach and Hilbert Spaces
4.5.5 Sturm-Liouville problem for equation X''-mu*X=0, case 2) Robin-Diriclet b.c.'s
4.6.2 Laplace's Equation Diriclet problem, basic case
4.6.2 8. Poisson's's Equation Diriclet problem
Heat Equation: 4.6.3 1) 1-d homogeneous equation and boundary conditions (Neumann-Neumann)
4.6.3 2) 1-d non-homogeneous equation and boundary conditions (Dirichlet-Dirichlet)
4.6.3 3) 1-d homogeneous equation and boundary conditions (Dirichlet-Robin) - application of Sturm-Liouville Theorem
4.6.3 4) 2-D temperature field in rectangular domain
Example of Diffusive Process: 
Wave Equation: 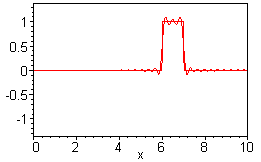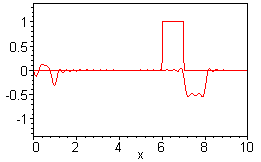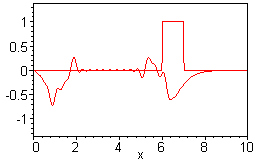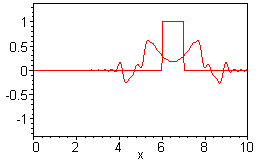 4.6.4 1) 1-d homogeneous equation and boundary conditions (Dirichlet-Robin)
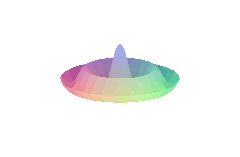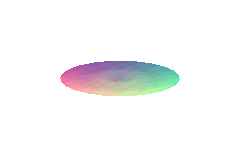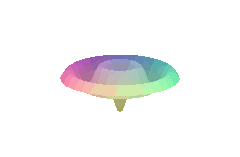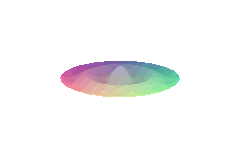 4.6.4. 2) vibration of circular membrane (standing waves)
4.6.6. Singular SLP: vibration of the ring 
Movies:
|
0
2
4
5
6
a
b
9
11
16
24
|
Special Functions |
Orthogonal Sets in Annular Domain: Table of Contents 1 Dirichlet-Dirichlet:
Maple:
nu=0
nu=1
2 Neumann-Dirichlet:
Maple:
nu=0
nu=1
3 Dirichlet-Neumann:
Maple:
nu=0
nu=1
4 Neumann-Neumann:
Maple:
nu=0
nu=1
5 Dirichlet-Robin:
Maple:
nu=0
nu=1
6 Neumann-Robin:
Maple:
nu=0
nu=1
7 Robin-Dirichlet:
Maple:
nu=0
nu=1
8 Robin-Neumann:
Maple:
nu=0
nu=1
9 Robin-Robin:
Maple:
nu=0
nu=1
|
9
Maple:
|
| Distributions |
|
||
| Integral Equations |
Lecture Notes
Lecture Notes (modified Feb 15, 2005: with Banach Fixed Point Theorem)
|
||
| Integral Transform Methods |
8.1 The Fourier Transform: Fourier Integral Representation(p.98) Wave Equation(p.105) Laplace's Equation (Poisson integral formula, p.107) Heat Equation (p.112) Laplace Equation (p.116) 8.2 The Laplace Transform: Solution of Heat Equation(p.121)  Solution of Wave Equation(p.123) 8.3 The Hankel Transform: Solution of Heat Equation(p.129)  Solution of Wave Equation(p.134) 8.4 Finite Fourier Transform: 8.4.2 Heat Equation in the Finite Layer(p.147) 8.4.3 Heat Equation in the Sphere(p.151) 8.6 Generalization of the Finite Integral Transform Method: 8.6.5 Transient Heat Transfer in the Fin(p.176) HW#5 (Wave Equation) |
||
| Mathematical Foundations of Signal Reconstruction |
|
||
| Mathematical Problems of Quantum Mechanics |
Harmonic Oscillator: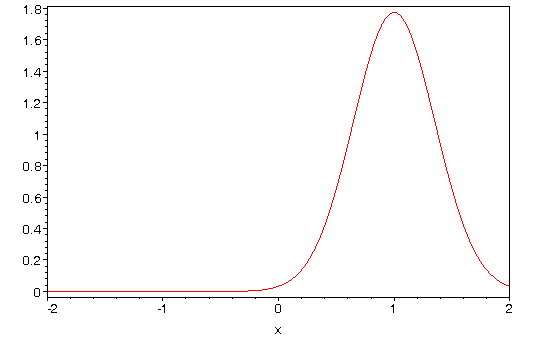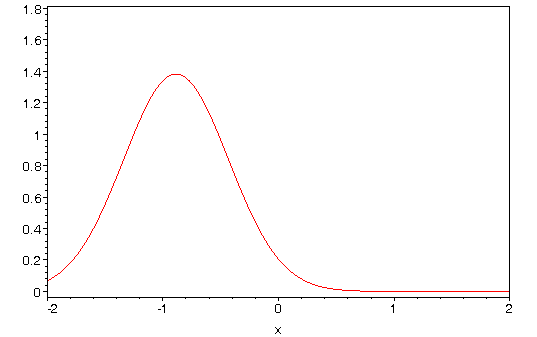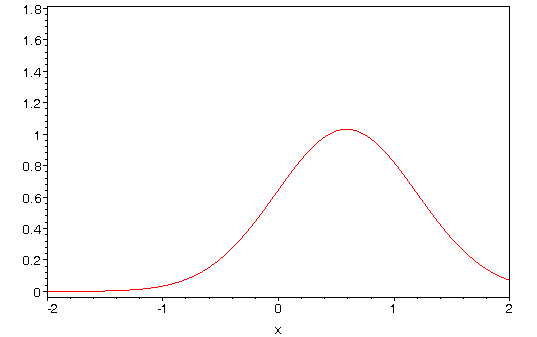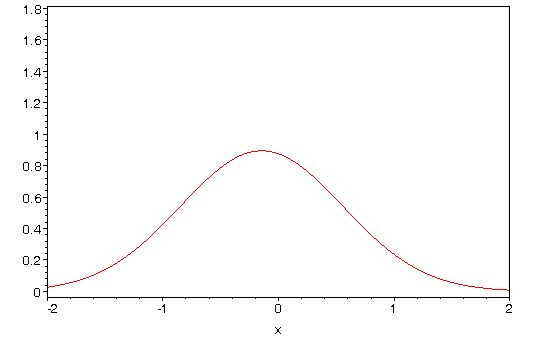 
Hydrogen Atom: 
|
||
| Complex Analysis |
|
|
Summary Tables |
|
All Tables 00 Table of Integrals 01 First Order ODE 02 Linear ODE 03 Power-Series Solution 05 Linear System of First Order ODE 06 Fourier Series 07 Hyperbolic Functions & Special Equation 08 Bessel Functions 09 Sturm-Liouville Theorem 10 Laplace Transform 11 Table of Laplace Transforms 12 Differentiation 14 Infinite Series 15 Complex Numbers 16 Integration 17 Limits 18 Heat Equation 20 Coordinate Systems 21 Greek Letters 22 Vectors in Euclidian Space |
|
GRADING |
|
Grading Criteria |
 |
|
Maple Guide Linear Algebra with Maple |
|
LINKS |
|
EngT295R Engineering Math Refresher Course EqWorld The World of Mathematical Equation The MacTutor History of Mathematics archive Math Aware Month Mathematics and Art |
|
INSTRUCTORS |
|
Dr. Reinhard O.W. Franz Dr. Vladimir P. Solovjov |
|
PHOTOS |
|
EngT 502 Winter 2001 EngT 502 Fall 2004 EngT 503 Winter 2005 EngT 502 Spring 2005 EngT 502 Fall 2005 |
|
Origin of the Name "Mathematics" |
|
Why is mathematics so named? |
|
|
|
Author Information |
|
VOLUME 1 APRIL 2005 |
|
Brian C. Liechty Non-Newtonian Behavior of a Rotating-Cylinder Induced Flow Laura Hansen The Cross Correlation: an Essential Mathematical Computation for Particle Imaging Velocimetry Craig Peterson A Review of Integral Equations Describing the Radial Distribution Function of Fluids Brady Woolford Analytical Solution to Steady State and Transient Flow in Ultrahydrophobic Channels Jason Thomas Solving Poisson's Equation on a Discrete Mesh |
|
VOLUME 2 JUNE 2005 |
|
Gifford Zach Decker 1D Momentum Integral Method (Thwaites) vs. 2D Finite Element Navier-Stokes Solution: Computing Flow Separtion, Flow Rate and Pressure Drop |
VOLUME 3 NOVEMBER 2005 |
|
Gary Kenneth Johns Modeling Piezoresistivity in Silicon and Polysilicon Daniel Karpowitz Bezier Curve Fitting Method for Existing Turbine Blade Design |
|
FINALS |
|
EngT502 Final Fall 2004 Part I Solution of problem #1 Maple Solution Solution of problem #2 Maple Solution  |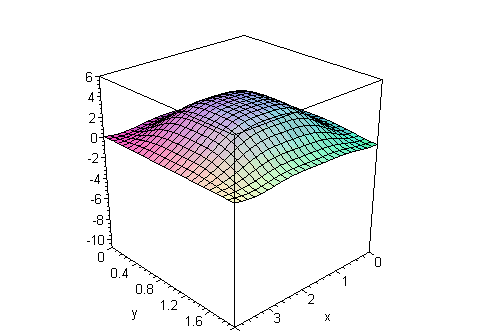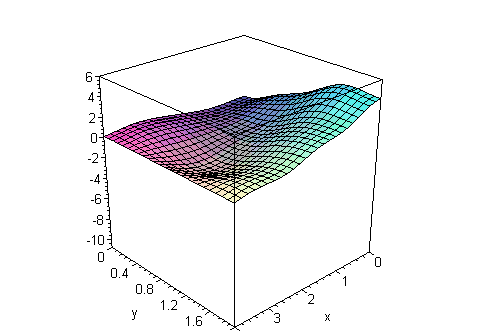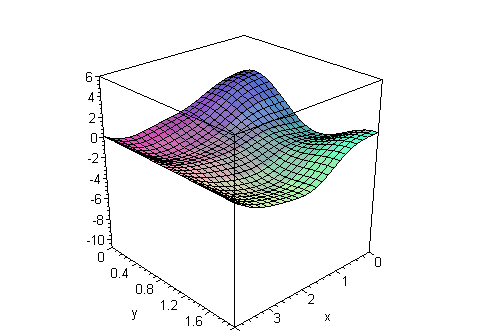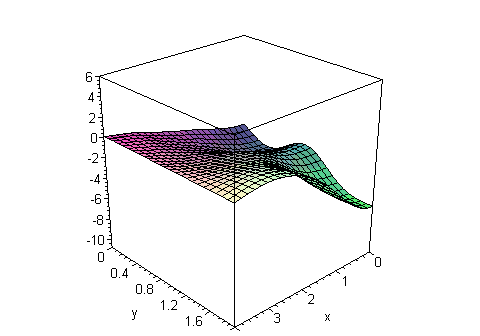
|
EngT503 Final Winter 2005 See new class photos and the first publications in the Journal of Applied Engineering Mathematics. Good Luck with Your Finals!!! Part I Quantum Mechanics Section: you can replace this problem by the problem of motion of Gaussian wave packet in 1-D or/and 2-D Coulomb's potential (Hydrogen atom or planetary motion in 1-D or 2-D microuniverse) with some visualization similar to the problem for harmonic oscillator (see Lecture Notes for Chapter 14 or ask me about the guidelines) Solution Maple Solution Vibration of the rectangular membrane with damping: 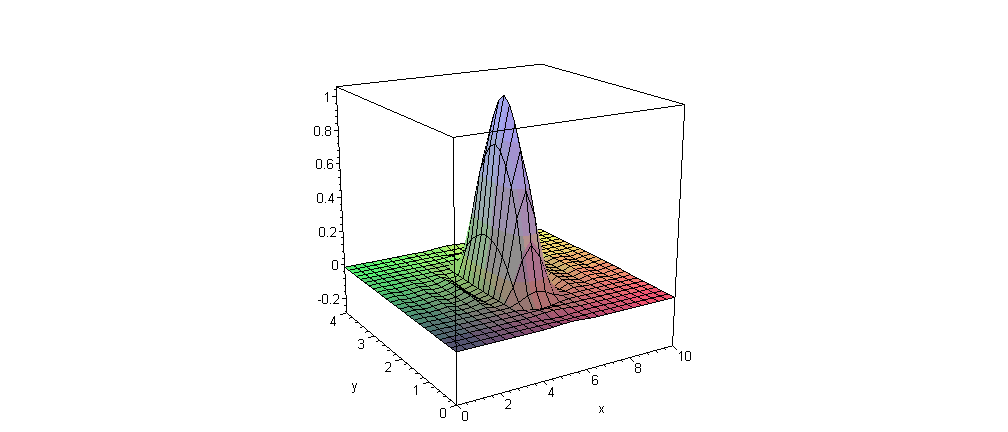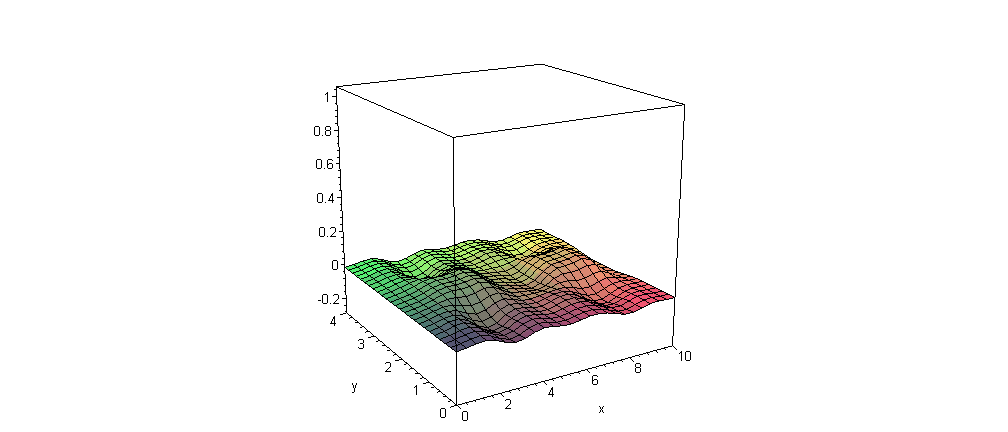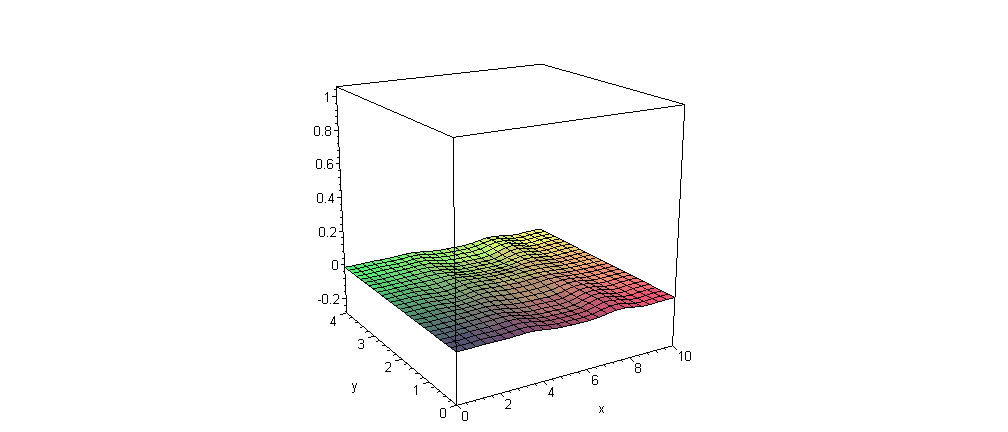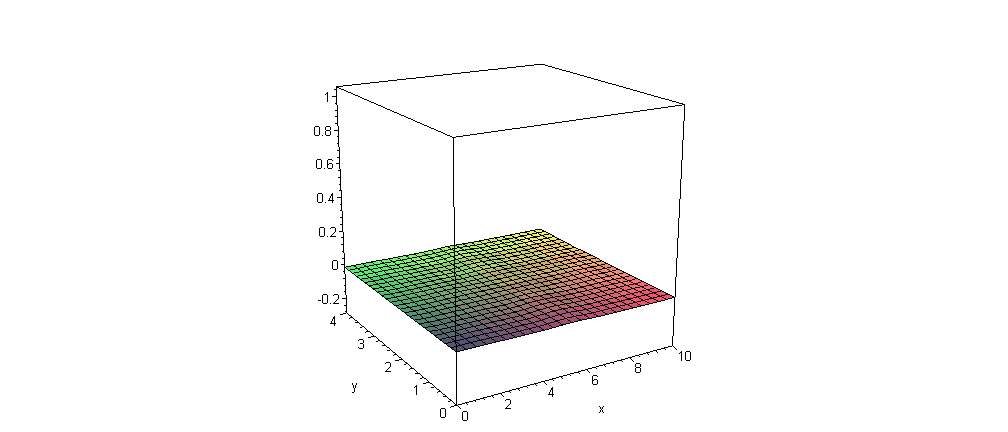 Part II |
|
EngT502 Final Spring 2005 Part I Solution of problem #1 Maple Solution Solution of problem #2 Maple Solution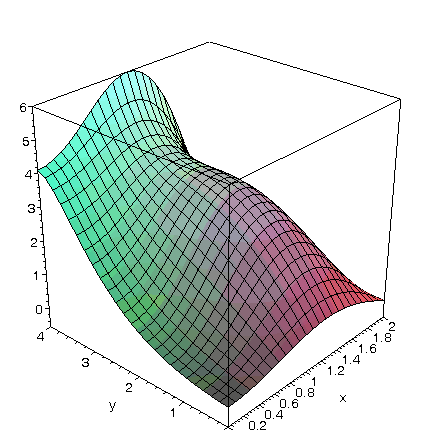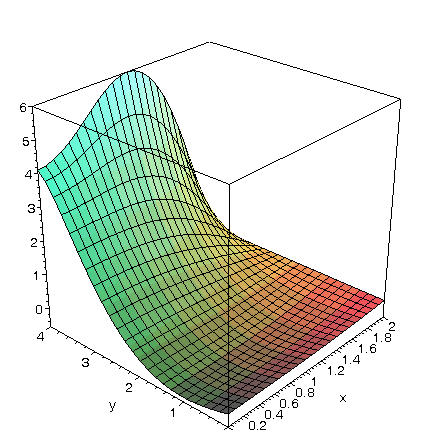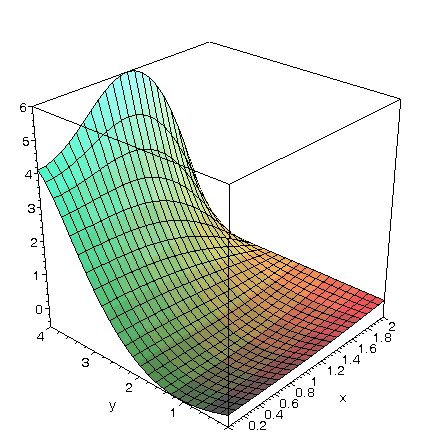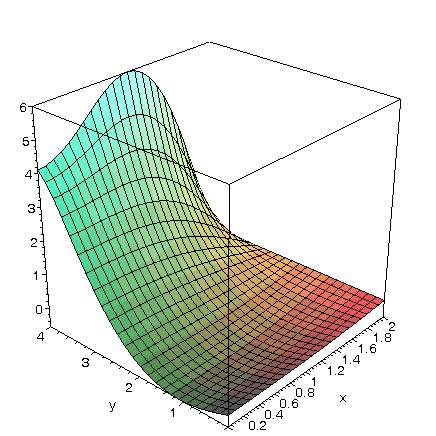 
Final Spring 2005 Part II Reed the paper of Gifford Decker in the 2nd Volume of JAEM Have a Good Summer! |
|
EngT502 Final FALL 2005: Project BB (Bouncing Ball) Maple Solution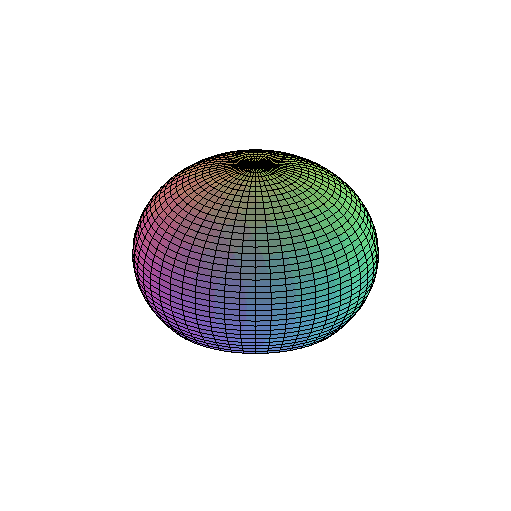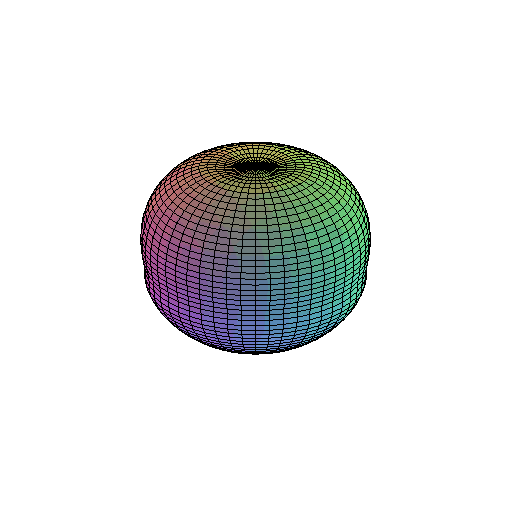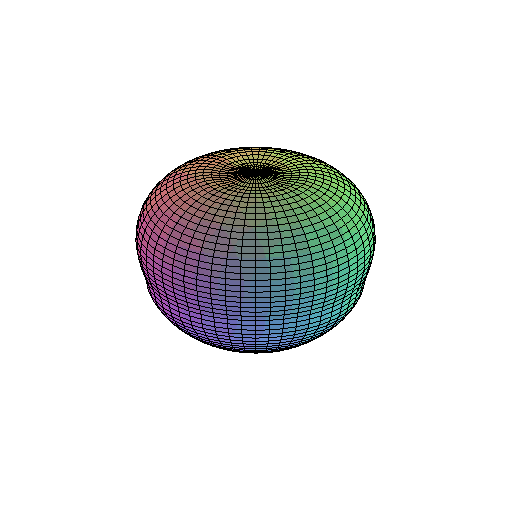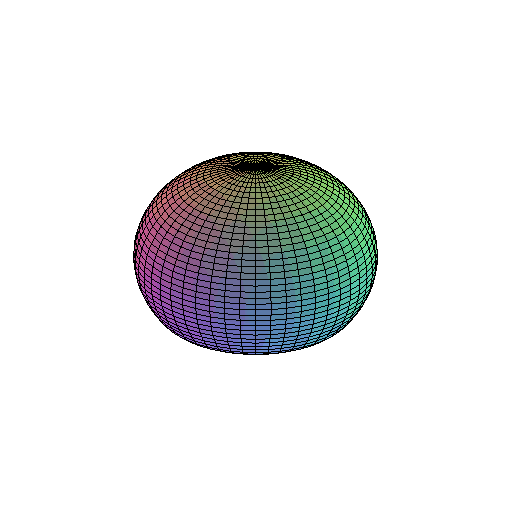 
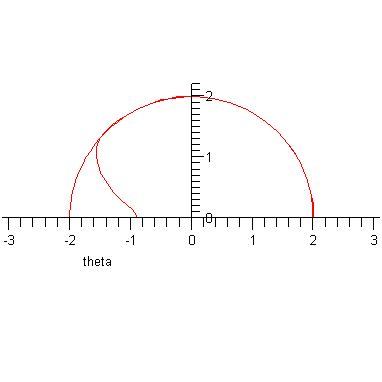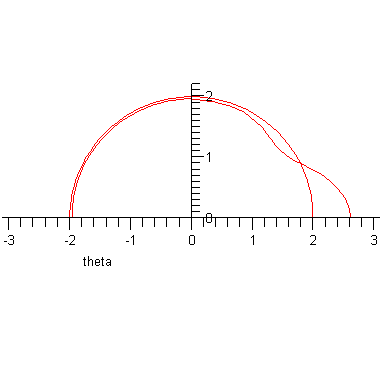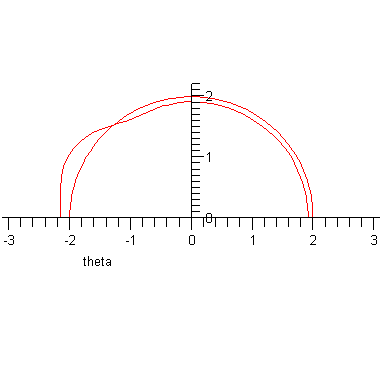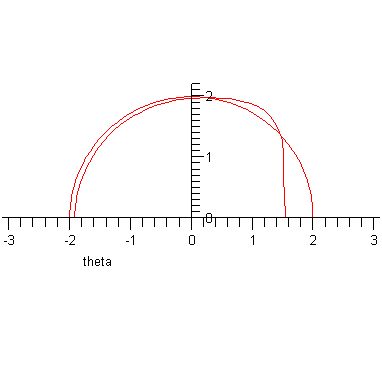
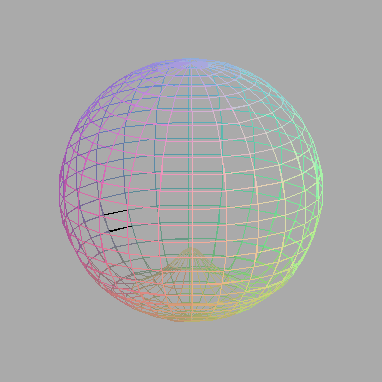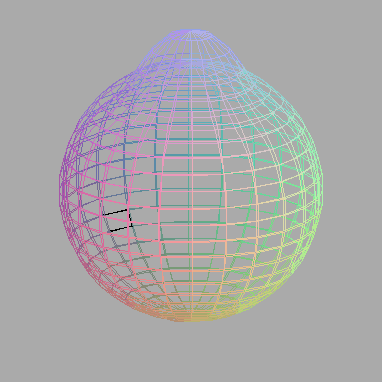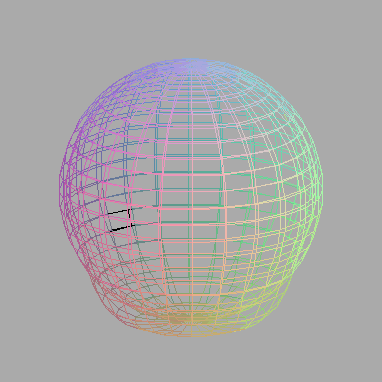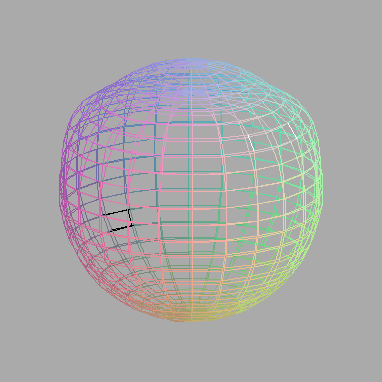
Solutions of Dan Karpowitz Final 2005 Part I Reed new papers in the 3rd Volume of JAEM Merry Christmas and Happy New Year! |
| PELE: POISSON'S EQUATION - LAPLACE'S EQUATION |
|
01 DDDD
02 NDDR
03 NNRD
04 DRND
05 RDDN
06 DDNR
07 DNRN
08 DDNN
09 DDRR
10 DNRR
11 RRDR
12 RNRR
13 RRNN
14 DRRD
15 RRRR
|
